Normal logarithms, signified by ln, are an essential idea in science, particularly in the fields of polynomial math and math. Equations involving exponential growth and decay, as well as a variety of mathematical modeling scenarios, rely heavily on them. Working on articulations including regular logarithms can every now and again uncover further bits of knowledge into the connections among numbers and make troublesome issues more sensible.
These articulations can be improved by utilizing logarithm properties like the item, remainder, and power rules. They are made easier to use and comprehend as a result. In this article, we will investigate how the saying: express as a single natural logarithm. ln 16 – ln 8 ln 2 ln 8 ln 128 can be executed, exhibiting the utilization of logarithmic properties to smooth out and work on numerical articulations.
What are the Properties of Logarithms?
To work on the given articulation, we really want to use a few critical properties of logarithms that are basic in polynomial math and math. We are able to manipulate and transform logarithmic expressions into simpler or more useful forms thanks to these properties.
Product’s Logarithm
An item’s regular logarithm is equivalent to the sum of its singular variables’ normal logarithms, according to this property. This can be mathematically expressed as:ln(a * b) = ln(a) + ln(b)
The logarithm of a Ratio
The difference between the regular logarithms of the numerator and the denominator corresponds to the normal logarithm of a remainder, as indicated by this property. Writing is possible.: ln(a / b) = ln(a) – ln(b)
The logarithm of a Power
This property demonstrates that the regular logarithm of a number raised to a power is equivalent to the power duplicated by the normal logarithm of the base number. It is symbolized by: ln(a^b) = b * ln(a)
We can methodically disassemble and reassemble logarithmic expressions by making use of these properties.
Step-by-Step Simplification of the Query
Here is the step-by-step simplification of the above query:
1. Product and Quotient Rules To Combine Log
You will see, ln 8 ln 2 ln 8 ln 128 is said to be a product of logarithms. We need to group and simplify them appropriately. First, we focus on simplifying the expression within the logs:
- ln 16 can be simplified as ln(2^4) = 4 * ln(2)
- ln 8 can be simplified as ln(2^3) = 3 * ln(2)
- ln 128 can be simplified as ln(2^7) = 7 * ln(2)
2. Substituting Simplified Values
Substituting these simplified values into the expression gives us: 4ln(2)−3ln(2)⋅ln(2)⋅3ln(2)⋅7ln(2)
3. Combining Like Terms
We can then combine like terms by recognizing that ln(2)⋅ln(2)⋅ln(2)⋅ln(2) can be expressed as (ln(2)\ln(2)ln(2))^4. Therefore, the expression becomes: 4ln(2)−3(ln(2))4⋅7
4. Simplifying Further
By recognizing the power rule and simplifying the coefficients: 4ln(2)−21(ln(2))4
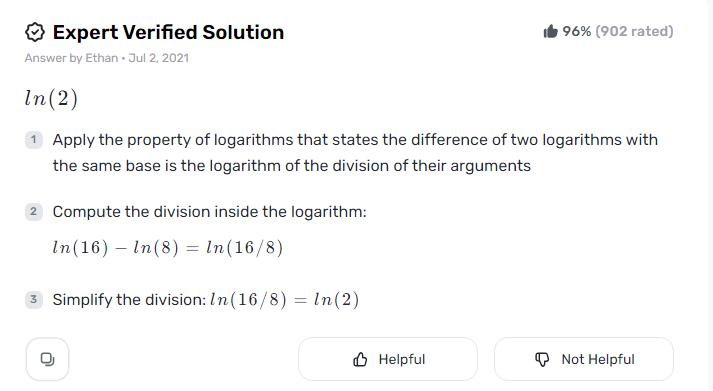
5. Expressing as a Single Natural Logarithm
Since we actually have a blend of terms as opposed to a solitary logarithm, further disentanglement relies upon the unique situation or extra requirements given in a particular issue. Notwithstanding, as a general methodology, the saying ln 16 – ln 8 ln 2 ln 8 ln 128, can be streamlined to the structure including powers of normal logarithms:
4ln(2)−21(ln(2))4
Steps for Using Gauth for Solving Math Queries
This is the way you can utilize Gauth really:
Step 1: Provide your Query
Either type your math question directly into the text field or upload an image of the problem to begin. The AI algorithms in Gauth are able to recognize mathematical expressions written down or printed, making them adaptable to any format.
Step 2. Get Your Answer
After entering your query, wait a while. Gauth will investigate the issue utilizing its high-level calculations and furnish you with an itemized arrangement. The arrangement will incorporate each step of the critical thinking process, making it simple for you to track and figure out the arrangement.
Step 3. Copy or Regenerate
Subsequent to getting the arrangement, you have the choice to duplicate the answer for your reference or recover new arrangements utilizing various varieties of the issue. When practicing similar problems or ensuring that the solution is correct, this feature is helpful.
Sum Up
Since we actually have a blend of terms as opposed to a solitary logarithm, further disentanglement relies upon the unique situation or extra requirements given in a particular issue. Notwithstanding, as a general methodology, the saying, ln 16 – ln 8 ln 2 ln 8 ln 128, can be streamlined to the structure including powers of normal logarithms.